Bye bye trees:

From downstairs (before)	From downstairs (during)	From downstairs (after)
From upstairs (before)	From upstairs (during)	From upstairs (after)
	Some of the logs on the driveway before pickup

(Permalink)

Some images from a Minecraft server I used to play on:

A far-out view	Same but from a different angle
A winter scene I made	Senate building and my HMS Victory out back
Massive village, swimming pool and Town of Salem	A tudor interpretation of my home

(Permalink)

I've seen a couple of things like this online, but I thought I'd create one of my own: a questionnaire tabletop RPG groups and GM's can use to get an idea as to what everyone is looking for out of the game. It's very easy for groups to get together and, after a few sessions, realise everyone's playing styles or preferences don't gel, or don't fit the setting the GM has come up with. Gathering info from the players ahead of time can help guide which RPG system to play, the settings of the world and the campaign they want to be involved in, as well as pertinent out of game information. With that in mind, here's my thoughts of a questionnaire that could help:

Are You Interested In Being Involved (As Player Or GM) In A Traditional / "Tabletop" Roleplaying Game?
If So, What Would You Like To See In It? Take A Look At The Categories Below And Rate Your Interest Levels.

(GM = Game Master, aka DM or Dungeon Master, NPC = Non-Player Character, an in-game character controlled by the GM)

In The Game: The Genre Or Setting Of The Game:

SETTING ["1" (really not interested) to "5" (very interested)]:

• Prehistoric
• Ancient Egypt / Greek / Rome
• Medieval Era Europe
• Feudal Japan
• Wild West
• Victorian Era Europe
• World War (I or II)
• Modern Day America / Japan
• Post Apocalypse
• The Moon / Mars
• Distant Stars / Galaxies
• Multiple Dimensions

CREATURES ["1" (really not interested) to "5" (very interested)]:

• Dinosaurs
• Mythological (gods & goddesses)
• World of Darkness / Peasant Horror (vampires, werewolves, witches, ghosts)
• Demons and Lovecraft-ian Horrors From The Beyond
• Tolkien-esque High Fantasy (elves, goblins, trolls, dragons)
• Realistic (just other people, animals)
• Sci-fi (robots, mechs, cyborgs)

ABILITIES ["1" (really not interested) to "5" (very interested)]:

• Magic
• Regeneration / Resurrection (minimal chance of scars, limb loss, permadeath)
• Psionics
• Steampunk / Mechanical
• Technological
• Cyberpunk
• Superhero
• Time Travel

WEAPONS ["1" (really not interested) to "5" (very interested)]:

• Claws, Fangs
• Martial Arts
• Swords, Bows
• Muskets, Cannons
• Pistols, Rifles
• Machine Guns, Tanks
• Ray Guns, AI-Controlled Drones

TRAVEL ["1" (really not interested) to "5" (very interested)]:

• On foot
• On horseback
• By caravan
• By boat
• By airship
• By car
• By plane
• By teleportation
• By spaceship
• By interdimensional portals

Outside The Game: The Mechanics Or Meta Of The Game:

CAMPAIGN ["1" (strongly disagree) to "5" (strongly agree)]:

• The campaign should have an end goal that players can reach to "win"
• The campaign should have obstacles, puzzles and opponents tailored to the characters playing it
• The campaign should have missions and quests that are long and convoluted
• The campaign should have a linear storyline
• The campaign should be pre-defined by the GM
• The campaign should be lore and history heavy
• The campaign should be a setting in conflict with the players (e.g. players are escaped convicts or part of a rebellion)
• The campaign should be focused in and around a single location
• The campaign should be bustling with people and interesting places everywhere
• The campaign should be combat focused
• The campaign should include random encounters
• The campaign should include downtime / social situations
• The campaign should include espionage and subterfuge
• The campaign should include royal and political intrigue
• The campaign should include lots of recurring / significant NPCs
• The campaign should include lots of NPCs with skills / classes the same as the characters
• The campaign should include lots of dungeon crawling
• The campaign should include lots of monster slaying
• The campaign should include lots of tricksy logic puzzles
• The campaign should include lots of things I've never seen before

CHARACTERS ["1" (strongly disagree) to "5" (strongly agree)]:

• Characters should be pre-generated and supplied by the GM
• Characters should be created using a system that involves dice rolling
• Characters should be exceptional compared to the average NPC
• Characters should be always good / heroic
• Characters should have motivations and backgrounds that are hidden from the other players
• Characters should have significant flaws as well as strengths
• Characters should start off low level
• Characters should start off as unknown nobodies
• Characters should start off with some background / pre-gaming (maybe one-on-one) exploration with the GM
• Characters should start off already knowing the other characters
• Characters should see their abilities increase as the campaign progresses (level, skills, health, power)
• Characters should see their social status increase as the campaign progresses (e.g. to guild leaders, kings, gods)
• Characters should have the chance to have NPCs under their control (e.g. servants or armies)
• Characters should expect to experience repercussions for their actions
• Characters should expect to survive the length of the campaign
• Characters should expect to reach some form of max level / skill cap before the campaign ends

GROUP ["1" (strongly disagree) to "5" (strongly agree)]:

• Players should be allowed to play more than one character at a time
• The group of players should be consistent from one session to the next
• The party should all work together
• The party should always stay together
• The party should have lots of internal conflicts
• The party should include some NPCs controlled by the GM
• The party should feel like they're in competition against the GM

RULESET ["1" (strongly disagree) to "5" (strongly agree)]:

• The ruleset should be clearly defined
• The ruleset should be expansive with lots of options and complexity
• The ruleset should numerically represent character skills, levels, health, etc.
• The ruleset should involve lots of dice rolling
• The ruleset should allow the success of actions to be influenced beyond just dice rolling (e.g. spending karma, willpower, re-rolls)
• The ruleset should allow for lots of secondary / non combat skills (e.g. cooking, artistry, sewing, navigation, speed reading)
• The ruleset should limit character abilities based upon choices made at character generation (e.g. race and class)
• The ruleset should include lots of detailed rulings (e.g. encumbrance limits, racial move speed differences)

ME ["1" (strongly disagree) to "5" (strongly agree)]:

• I like playing characters that break the mould
• I like verbally roleplaying as my character
• I like roleplaying meetings with NPCs
• I like having private conversations about things with other players or the GM
• I like roleplaying the personality of my character, even if the actions are detrimental to the current situation
• I like min-maxing (squeezing every bonus from my character setup and ruleset in order to win situations)
• I like being able to do things the other characters can't do
• I like knowing things the other players don't know
• I like meta-gaming (utilising knowledge outside my character's knowledge)
• I like knowing and having access to all the rules of the game we're playing
• I like arguing over the rules
• I like comparing my progress to that of the other players
• I like outcomes from dice rolls to be final
• I like getting powerful loot drops from encounters
• I like keeping detailed notes on my character's inventory and wealth status
• I like seeing and playing with pre-drawn maps and miniatures

Finally:

• The game should have (in addition to a GM): 1-2 players / 3-4 players / 5-6 players / as many players as possible
• The game should have sessions that last: an hour / a couple of hours / hours and hours and hours
• The game should have sessions: every week / every two weeks / every month
• The game should come to a conclusion after: one session / several sessions / several months / as long as humanly possible

(Permalink)

So, recently I just finished reading The Picture of Dorian Gray the other week. My conclusion: I don't think I would have liked Oscar Wilde as a person much.

I've never read the book before, and the majority of my previous knowledge about Oscar Wilde is based on the trials that focused on his personal life. A victim of the era he was born into, a can sympathise with him from that angle. However, as an author, this book has not endeared me to his writing style.

Okay, it's clearly provocative, again riling against the tight laced practices of the Victorian age. However, for a book that is clearly striving to highlight and promote the concepts of decadence, flamboyance, and art over practicality, I found the book itself to border on tedium in too many places. There's a whole chapter which is just clearly Wilde boasting of his own literary knowledge, which is boring in the extreme. There seems no real redemption for any of the flawed characters (which gives no reason for me to care as to whether they come to a good or bad end), and they all deride the working class and practical professions of the time, without the narrative giving any indication that the reader should believe otherwise themselves. There's a period where almost two decades pass and we're only given the flimsiest of suggestions that he's done "bad things" in the intervening years, and the book ends too suddenly after Dorian's death.

All in all, I feel like this is a self indulgent book by the author where the reader comes away feeling as if Wilde wishes he could have been more Dorian-like himself. It's worth reading because of its classic status and to maybe get an idea of the clash of certain Victorian cultures, but I know I won't be reading this again, and I'm less sympathetic towards its author than I was before picking it up.

(Permalink)

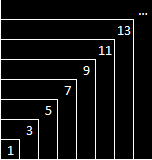
Is there anything remarkable about the fact that 3² + 4² = 5²?

A couple of random mathematical conversations occurred at work the other week, during one of which the above equation was mentioned (it's a commonly known integer solution for a right angle triangle). It was noted that some people find it too coincidental that things like the above are true. Personally, I'm of the reverse opinion. There's a million other equations we could test for small numbers that wouldn't turn out to be true, it's just this one is. It might seem interesting, but is there really anything unique about it...?

Let's have a meandering chat about some mathematical concepts:

There's An Infinite Number Of Numbers

This is a pretty trivial statement that most people come across early in their school days. The proof? It's simply that if you think there's a "biggest number" we can always add 1 to it to make an even bigger one. For ever. Not much to say here, but let's throw around some basic stuff first.

The Sum Of The First N Odd Numbers Is A Square

This is another one that's relatively simple to demonstrate:

 1 = 1² = 1
 4 = 2² = 1 + 3
 9 = 3² = 1 + 3 + 5
16 = 4² = 1 + 3 + 5 + 7
25 = 5² = 1 + 3 + 5 + 7 + 9
36 = 6² = 1 + 3 + 5 + 7 + 9 + 11
49 = 7² = 1 + 3 + 5 + 7 + 9 + 11 + 13
... and so on.

Basically, start from 1 and add the next odd number, and the next, and the next, and... Do this as many times as you like and you will always end up with a square number. Further, for any odd number there's some square number which if you add that odd number to it will also result in a square (e.g. for odd number 13, 7² = 6² + 13).

Combine The Two

So, what can get from the two topics above?

Well, from the first point we know there's obviously an infinite amount of odd numbers. Let's call one of those numbers X. X² is also an odd number.

And from our second point, we know there's always some square number Y² such that the (Y+1)² = Y² + X².

With a bit of magic maths, we can get a bit further than this too. I'll leave it as an exercise for the reader, but with some number crunching we can relatively easily determine that for a given X in the above equation, Y = (X² - 1) / 2.

Let's start calculating some of these:

5² = 4² + 3²
13² = 12² + 5²
25² = 24² + 7²
41² = 40² + 9²
61² = 60² + 11²
85² = 84² + 13²
... and so on.

So, basically, our original formula is just one of an infinite number of "right angled triangle" solutions, all following a regular pattern where the two longest sides differ by just one unit.

In Summary

You might still feel that 3/4/5 is still worthy of consideration as being a special and unique case though. After all, no other solutions form a sequence of three numbers, right? And it's the first solution for the equation?

Well, maybe... If it weren't for that fact that 1² = 0² + (-1)².

Recommended further reading: Fermat's Last Theorem

(Permalink)