| Home |
| Blog |
| The Geek |
| Books |
| Movies |
| Video Games |
| Board Games |
| Music |
| Philip Reed |
| < Newer Posts | Older Posts > |
 | 23rd February, 2013 |  | |||
 |  |  | |||
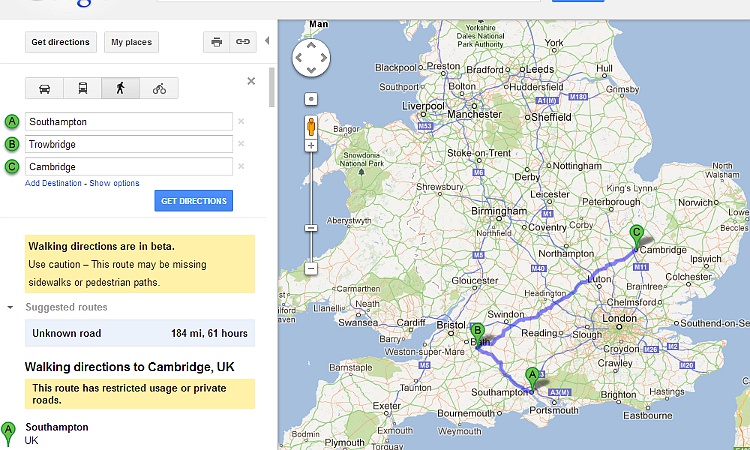
 | So, according to Google Maps, a walk from Southampton to Cambridge via Trowbridge would be roughly 180 miles in length.
I reckon if someone were to wander that route, not making any particular effort to speed-walk or anything, that could accomplished in a couple of weeks pretty simply. Just sayin'... |  | |||
 |  |  | |||


 | 15th December, 2012 |  | ||
 |  |  | ||
 | So, apparently (according to my family), one does not simply "pop" over to Bulgaria for a business trip. "Pah!", I say to them! "Pah!" |  | ||
 |  |  | ||

 | 6th December, 2012 |  | ||
 |  |  | ||
 | Things I learnt from my recent Reddit post:
|  | ||
 |  |  | ||

 | 1st December, 2012 |  | ||
 |  |  | ||
 | Okay, let's see how Site5 holds up. I don't know what level of traffic I'm going to see, but there was no way I was going to risk running a competition on my old Demon site, that's for sure. |  | ||
 |  |  | ||

| < Newer Posts | Older Posts > |